Printre alte căutări ale mele, veți găsi aici și germenii unei noi Fizici, bazate pe forma elicoidală a traiectoriilor. În Fizica elicoidală repausul și mișcarea rectilinie sunt imposibile (pentru că duc la paradoxul informațional). În Fizica elicoidală corpurile libere se mișcă pe o elice, nu pe o dreaptă.
Motto: „Trebuie să supui îndoielii tot ce poate fi pus la îndoială, doar astfel se poate descoperi ce nu poate fi pus la îndoială.” (Tadeusz Kotarbiński)
Căutați ceva anume?
sâmbătă, 28 decembrie 2013
marți, 24 decembrie 2013
Corespondenţa biunivocă dintre elicele circulare şi numerele complexe
Bazându-ne pe observaţia că oricărei perechi formate cu torsiunea şi curbura unei curbe într-un anumit punct al ei îi putem asocia un număr complex, numit „torsiune complexă”, putem duce aceste raţionamente mai departe şi să construim o altă asociere, de data aceasta între o elice circulară şi un număr complex.
Mai precis, având în vedere faptul că torsiunea şi curbura unei elice circulare sunt constante, putem asocia unei elice circulare tocmai numărul complex  , format cu torsiunea şi curbura acelei elice. Prin această asociere, fiecare elice circulară este un punct în planul complex. Şi reciproc, fiecărui punct din planul complex îi asociem elicea circulară cu torsiunea dată de partea reală a numărului complex dat de afixul punctului respectiv din planul complex şi curbura dată de partea imaginară a acestui număr complex.
, format cu torsiunea şi curbura acelei elice. Prin această asociere, fiecare elice circulară este un punct în planul complex. Şi reciproc, fiecărui punct din planul complex îi asociem elicea circulară cu torsiunea dată de partea reală a numărului complex dat de afixul punctului respectiv din planul complex şi curbura dată de partea imaginară a acestui număr complex.
Desigur, nu toate elicele sunt elice circulare. Deci, nu oricărei elice îi putem asocia un punct. Dar, cu certitudine, oricărei elice îi putem asocia o mulţime de numere complexe cu acelaşi argument. Aşadar, unei elice oarecare îi asociem în planul complex un segment de dreaptă înclinat faţă de axa absciselor cu un unghi egal cu argumentul torsiunii complexe. Acest lucru exprimă şi faptul că o curbă de lancretian constant (deci o elice) poate fi considerată în planul complex un segment de dreaptă a cărui prelungire trece prin origine.
Complementar, putem vorbi despre curbe de darbuzian constant, acestea având ca reprezentare în planul complex nişte arce de cerc cu centrul în origine. Asemenea curbe, deşi au lancretianul variabil, au proprietăţi identice numerelor complexe de modul constant. Altfel spus, putem stabili un izomorfism între mulţimea curbelor de darbuzian constant şi a numerelor complexe de modul constant, aşa cum putem stabili un izomorfism între mulţimea curbelor de lancretian constant şi mulţimea numerelor complexe de argument constant.
Printr-o transformare conformă, putem înlocui planul complex cu un plan în care pe axa absciselor să reprezentăm valorile lancretianului, iar pe axa ordonatelor să reprezentăm valorile darbuzianului. Într-un asemenea plan, elicele circulare ar rămâne puncte, elicele ar fi segmente „verticale”, iar curbele de darbuzian constant (oare ce denumire să dăm unor asemenea curbe?) ar fi segmente „orizontale”.
marți, 17 decembrie 2013
Distincţia dintre impuls şi impulsul elicoidal ar putea concilia Fizica cuantică şi Teoria relativităţii
În articolul precedent am arătat care este deosebirea fundamentală dintre Fizica elicoidală şi Fizica actuală, clarificând faptul că această deosebire constă în distincţia dintre impuls şi impulsul elicoidal. Aici doresc să scot în evidenţă posibilitatea de a concilia Fizica cuantică şi Teoria relativităţii cu ajutorul distincţiei dintre impuls şi impulsul elicoidal.
Consider că incompatibilitatea actuală dintre Fizica cuantică şi Teoria relativităţii ar putea fi eliminată dacă am conştientiza că cele două Fizici se referă fiecare la al impuls. Mai precis, presupun că în timp ce Fizica cuantică se referă la impuls în consideraţiile sale, Teoria relativităţii se referă de fapt la impulsul elicoidal. Aşadar, cele două Fizici înţeleg noţiunea de impuls fiecare în felul lor.
Fizica cuantică, având acces la instrumente mai precise pentru determinarea traiectoriei, constată că impulsul este proporţional cu tangenta la traiectoria particulei. Pe când, Teoria relativităţii preia noţiunea de impuls aşa cum vine ea de la Newton, din domeniul macroscopic, unde nu putem determina cu precizie suficientă forma traiectoriei.
Ia vedeţi ce iese de aici!
duminică, 15 decembrie 2013
Deosebirea fundamentală între Fizica elicoidală şi Fizica actuală
Există
o singură mare diferenţă între Fizica elicoidală şi Fizica actuală. Din
aceasta derivă toate celelalte. Voi discuta mai jos despre ea.
Ştim că unei traiectorii îi putem asocia triedrul lui Frenet (dat de versorii tangentă, normală şi binormală) şi îi mai putem asocia vectorul lui Darboux (dat de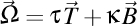 ).
În acest context, Fizica actuală consideră că impulsul unui corp este
proporţional (şi deci paralel) cu tangenta la traiectorie, adică cu
versorul
).
În acest context, Fizica actuală consideră că impulsul unui corp este
proporţional (şi deci paralel) cu tangenta la traiectorie, adică cu
versorul 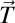 .
.
Ei bine, Fizica elicoidală spune că, dimpotrivă, impulsul unui corp nu este proporţional cu tangenta la traiectorie, ci tocmai cu vectorul lui Darboux! Mai exact, în Fizica elicoidală, impulsul unui corp (pe care îl putem numi impuls elicoidal) este tocmai produsul dintre constanta lui Planck şi vectorul lui Darboux. Adică, avem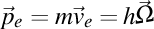 . Aceasta este singura
deosebire fundamentală dintre cele două teorii! Toate celelalte noţiuni
trebuie adaptate la această deosebire. De exemplu, forţa elicoidală va
fi derivata în raport cu timpul a impulsului elicoidal.
. Aceasta este singura
deosebire fundamentală dintre cele două teorii! Toate celelalte noţiuni
trebuie adaptate la această deosebire. De exemplu, forţa elicoidală va
fi derivata în raport cu timpul a impulsului elicoidal.
Observăm că dacă torsiunea traiectoriei este uriaşă (sau curbura foarte mică), atunci impulsul elicoidal devine aproape paralel cu impulsul (neelicoidal), iar distincţia dintre cele două mărimi fizice vectoriale devine imposibilă. Acesta este cazul corpurilor macroscopice, a căror masă este uriaşă. Pentru corpurile microscopice, distincţia începe să capete contur din ce în ce mai evident, pe măsură ce unghiul dintre versorul tangentă şi vectorul lui Darboux creşte.
Să mai observăm că forţa elicoidală este de două tipuri: forţă care modifică numai modulul impulsului elicoidal (deci numai darbuzianul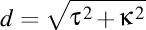 , constanta lui Planck fiind o constantă)
şi forţă care modifică numai direcţia impulsului elicoidal, deci forţă
care abate traiectoria de la forma ei de elice (fapt care se poate
obţine numai modificând lancretianul, adică
, constanta lui Planck fiind o constantă)
şi forţă care modifică numai direcţia impulsului elicoidal, deci forţă
care abate traiectoria de la forma ei de elice (fapt care se poate
obţine numai modificând lancretianul, adică 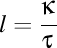 ). Aşadar, forţele elicoidale sunt doar de două tipuri: forţe darbuziene şi forţe lancretiene.
). Aşadar, forţele elicoidale sunt doar de două tipuri: forţe darbuziene şi forţe lancretiene.
Ştim că unei traiectorii îi putem asocia triedrul lui Frenet (dat de versorii tangentă, normală şi binormală) şi îi mai putem asocia vectorul lui Darboux (dat de
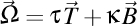 ).
În acest context, Fizica actuală consideră că impulsul unui corp este
proporţional (şi deci paralel) cu tangenta la traiectorie, adică cu
versorul
).
În acest context, Fizica actuală consideră că impulsul unui corp este
proporţional (şi deci paralel) cu tangenta la traiectorie, adică cu
versorul 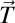 .
. Ei bine, Fizica elicoidală spune că, dimpotrivă, impulsul unui corp nu este proporţional cu tangenta la traiectorie, ci tocmai cu vectorul lui Darboux! Mai exact, în Fizica elicoidală, impulsul unui corp (pe care îl putem numi impuls elicoidal) este tocmai produsul dintre constanta lui Planck şi vectorul lui Darboux. Adică, avem
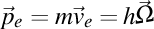 . Aceasta este singura
deosebire fundamentală dintre cele două teorii! Toate celelalte noţiuni
trebuie adaptate la această deosebire. De exemplu, forţa elicoidală va
fi derivata în raport cu timpul a impulsului elicoidal.
. Aceasta este singura
deosebire fundamentală dintre cele două teorii! Toate celelalte noţiuni
trebuie adaptate la această deosebire. De exemplu, forţa elicoidală va
fi derivata în raport cu timpul a impulsului elicoidal.Observăm că dacă torsiunea traiectoriei este uriaşă (sau curbura foarte mică), atunci impulsul elicoidal devine aproape paralel cu impulsul (neelicoidal), iar distincţia dintre cele două mărimi fizice vectoriale devine imposibilă. Acesta este cazul corpurilor macroscopice, a căror masă este uriaşă. Pentru corpurile microscopice, distincţia începe să capete contur din ce în ce mai evident, pe măsură ce unghiul dintre versorul tangentă şi vectorul lui Darboux creşte.
Să mai observăm că forţa elicoidală este de două tipuri: forţă care modifică numai modulul impulsului elicoidal (deci numai darbuzianul
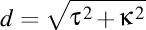 , constanta lui Planck fiind o constantă)
şi forţă care modifică numai direcţia impulsului elicoidal, deci forţă
care abate traiectoria de la forma ei de elice (fapt care se poate
obţine numai modificând lancretianul, adică
, constanta lui Planck fiind o constantă)
şi forţă care modifică numai direcţia impulsului elicoidal, deci forţă
care abate traiectoria de la forma ei de elice (fapt care se poate
obţine numai modificând lancretianul, adică 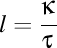 ). Aşadar, forţele elicoidale sunt doar de două tipuri: forţe darbuziene şi forţe lancretiene.
). Aşadar, forţele elicoidale sunt doar de două tipuri: forţe darbuziene şi forţe lancretiene.
joi, 5 decembrie 2013
Principiul elicoidal al inerţiei şi briciul lui Occam
Ştim cu toţii că principiul actual al inerţiei spune că un corp asupra căruia nu acţionează influenţe din exterior îşi menţine starea de repaus sau de mişcare rectilinie şi uniformă. Observaţi că această formulare conţine o disjuncţie de două propoziţii. Adică, principiul actual al inerţiei spune ceva de genul: dacă P atunci (Q sau R). Să notăm acest (Q sau R) cu S. Atunci, P este propoziţia „Asupra unui corp nu acţionează influenţe din exterior”, Q este propoziţia „Corpul îşi menţine starea de repaus”, iar R este propoziţia „Corpul îşi menţine starea de mişcare rectilinie şi uniformă”.
În acest context, reamintim ce spune principiul elicoidal al inerţiei, pentru a-l compara cu principiul actual al inerţiei.
Principiul elicoidal al inerţiei (sau Principiul elico-inerţiei): un corp asupra căruia nu acţionează influenţe din exterior îşi menţine starea de mişcare pe o elice circulară.
În acest context, reamintim ce spune principiul elicoidal al inerţiei, pentru a-l compara cu principiul actual al inerţiei.
Principiul elicoidal al inerţiei (sau Principiul elico-inerţiei): un corp asupra căruia nu acţionează influenţe din exterior îşi menţine starea de mişcare pe o elice circulară.
- Să observăm în primul rând faptul că principiul elicoidal al inerţiei nu mai conţine vreo disjuncţie de genul (Q sau R). Căci principiul elicoidal al inerţiei poate fi pus sub forma „dacă P atunci S”, unde S nu mai este o disjuncţie de propoziţii, ci este propoziţia „Corpul îşi menţine starea de mişcare pe o elice circulară”. Acesta este un prim semn de superioritate al acestui principiu faţă de principiul actual. Prin această proprietate, principiul elicoidal al inerţiei este mai simplu, mai economic, deci mai apropiat de natură. Acesta ar fi deja un prim criteriu serios pentru a fi luat în considerare (briciul lui Occam).
- Un alt criteriu de superioritate al acestui nou principiu este generalitatea lui. Principiul elicoidal al inerţiei spune inclusiv ceea ce spune principiul actual, dar spune chiar mai multe lucruri.
- Să arătăm întâi că spune inclusiv ceea ce spune principiul actual al inerţiei. Pentru aceasta va trebui să arătăm că atât repausul, cât şi mişcarea rectilinie şi uniformă pot fi considerate ambele ca fiind de fapt tocmai mişcare pe elice circulară.
- Este suficient să observăm că o elice circulară alungită la infinit este tocmai o dreaptă. Astfel, mişcarea rectilinie şi uniformă poate fi interpretată cu certitudine ca fiind mişcare pe o elice circulară alungită la infinit.
- De asemenea, este suficient să observăm că o elice circulară înghesuită într-un punct este tocmai „traiectoria repausului”. Desigur, operaţia de „înghesuire” este tocmai operaţia inversă celei de „alungire”. Când alungim o elice circulară până când ea devine o dreaptă, îi micşorăm curbura şi torsiunea până când acestea devin nule, iar când înghesuim elicea circulară până când aceasta devine un punct, îi mărim aceşti parametri până când aceştia devin infiniţi. În termenii Fizicii elicoidale, dreapta are darbuzianul nul, iar punctul are darbuzianul infinit.
- Să arătăm acum că principiul elicoidal al inerţiei spune mai multe lucruri decât spune principiul actual al inerţiei, cu toate că foloseşte mai puţini termeni. Este suficient să observăm că, aşa cum am arătat mai sus, principiul actual al inerţiei spune de fapt că un corp nesupus influenţelor externe se va mişca pe o elice circulară de darbuzian nul sau infinit. În acest context, principiul elicoidal al inerţiei spune că un corp nesupus influenţelor externe se va mişca pe o elice circulară de darbuzian constant, indiferent că acesta este nul, finit sau infinit. Mai mult, elicea circulară are şi lancretianul (raportul dintre curbură şi torsiune) constant, nu doar darbuzianul. Aşadar, principiul elicoidal al inerţiei aduce mai multe informaţii concrete despre traiectoria unui corp liber.
Sper ca aceste observaţii să contribuie mai eficient la adâncirea înţelegerii voastre privind acest principiu al Fizicii viitorului.
Abonați-vă la:
Postări (Atom)
Postări populare
-
Imaginaţi-vă două drepte coplanare şi concurente. Dacă unghiul dintre ele nu este un unghi drept, atunci proiecţia unei drepte pe cealaltă...
-
Se ştie că dacă lăsăm împreună două sisteme cu temperaturi diferite, atunci cele două sisteme vor interacţiona în mod ineluctabil cel puţin ...
-
P e forumuri în luna august 2010 Pe topicul „ Unificarea câmpurilor ” [quote="gheorghe adrian"]Pe noi insa ne intereseaza ai...
-
Problema eterului Problema eterului În a doua jumătate a secolului trecut, pe baza unor calcule matematice de o rară frumuseţe, fizicia...
-
Pe forumuri în săptămâna 19.04.2010-25.04.2010 Pe topicul „ Vulcanul Eyjafjallajokull ” Superbe probleme pui, mm şi cred că merită să găsim ...
-
Majoritatea oamenilor consideră că răspunsul la această întrebare a fost deja dat: Dumnezeu a creat Universul. Pentru aceştia, Dumnezeu este...
-
Pe topicul „ Energia cinetică în cădere spre o gaură neagră ” Dacă tot e să scoatem în evidenţă pseudoştiinţa cu atâta zel pe aici, atu...
-
Oare chiar este adevărat acest lucru pe care îl repet atât de des? Oare chiar este adevărat că oamenii sunt extrem de valoroși? Care oameni?...
-
După niște peripeții în care am primit vestea tristă de la elefant.ro că stocul s-a epuizat, azi am primit, în sfârșit, cartea impresionantă...
-
În această lucrare prezint cititorilor într-o manieră simplă un procedeu care permite calcularea sumelor de forma altfel decât apelând la ...
Arhivă blog
-
►
2023
(15)
- ► septembrie (2)
-
►
2022
(13)
- ► septembrie (2)
-
►
2021
(20)
- ► septembrie (3)
-
►
2016
(19)
- ► septembrie (2)
-
►
2012
(56)
- ► septembrie (7)
-
►
2011
(67)
- ► septembrie (5)
-
►
2010
(99)
- ► septembrie (17)
-
►
2009
(32)
- ► septembrie (3)
-
►
2008
(25)
- ► septembrie (1)
Etichete
- Cercetări (114)
- Fizică elicoidală (86)
- Pe forumuri (86)
- Rezultate (75)
- Diverse (52)
- Fundamente (52)
- Noţiuni noi (28)
- Filosofie (24)
- Formulele lui Frenet (23)
- Întrebări (23)
- Articles in English (21)
- Ipoteze (21)
- Principiul inerţiei (19)
- Definiţii (18)
- Impuls (18)
- Torsiune (18)
- Elice (17)
- Lancretian (17)
- Curbură (16)
- Postulate (16)
- Câmp gravitaţional (15)
- Axiomatizare (14)
- Curbă închisă (14)
- Câmp magnetic (11)
- Personal (11)
- Teorema de recurenţă (11)
- Traiectorie (11)
- Baricentru (9)
- Principiul echivalenţei (9)
- Stabilitate (9)
- Articole publicate în revista „Evrika” (8)
- Darbuzian (8)
- Găuri negre (8)
- Matematică (8)
- Punct fizic (8)
- Corp solid (7)
- Dreaptă (7)
- Probleme (7)
- Termodinamică (7)
- Viteza medie (7)
- Anomalia Pioneer (6)
- Aproximare (6)
- Foton (6)
- Impuls volumic (6)
- Informație (6)
- Materializare (6)
- Maxima (6)
- Observator (6)
- Precesia (6)
- Valoarea oamenilor (6)
- Câmp vectorial (5)
- Discrepanţa dintre bogaţi şi săraci (5)
- Dreapta caracteristică (5)
- Fizica cuantică (5)
- Gravitație (5)
- Imposibilitatea repausului (5)
- Moment cinetic (5)
- Principiul relativității (5)
- Teoria relativităţii (5)
- Turbulenţa (5)
- Viteză (5)
- Ciocnire (4)
- Experimente (4)
- Mișcare elicoidală (4)
- Număr complex (4)
- Rezonanță (4)
- Satelizare (4)
- Big Bang (3)
- Componentele elicoidale (3)
- Darbuzor (3)
- Dimensiuni (3)
- Elicea închisă (3)
- Forţe (3)
- Fulger (3)
- Interferența (3)
- Masă (3)
- Plan de masă (3)
- Pseudoştiinţă (3)
- Rază etalon (3)
- Reper (3)
- Sarcină electrică (3)
- Stări de agregare (3)
- Teoria corpusculară (3)
- Torsiune complexă (3)
- Viteză volumică (3)
- Axa curbei (2)
- Calculator (2)
- Clasificare (2)
- Conspiraţie (2)
- Energie (2)
- Faza lichidă (2)
- Frecare (2)
- Galaxii (2)
- Lagrangean (2)
- Logică (2)
- Luxon (2)
- Materia întunecată (2)
- Moartea termică (2)
- Modelare (2)
- Ordine (2)
- Particule (2)
- Substanță (2)
- Transformările Lorentz (2)
- Triedrul lui Frenet de ordinul al doilea (2)
- Undă de probabilitate (2)
- Vectori (2)
- Viteza luminii (2)
- generalized helix (2)
- Amplitudine (1)
- Antimaterie (1)
- Apelul la autoritate (1)
- Asteroizi (1)
- Axa diavolului (1)
- Bobină (1)
- Curbură complexă (1)
- Curent electric (1)
- Câmp (1)
- Cărți (1)
- Democrația prin internet (1)
- Echilibru (1)
- Elice circulară (1)
- Elice perfectă (1)
- Forța de frecare (1)
- Forțe longitudinale (1)
- Forțe transversale (1)
- Inelon (1)
- Jet (1)
- Jgheabul lui AdiJapan (1)
- Kepler (1)
- Lecturi (1)
- Linii de câmp (1)
- Lucru (1)
- Lumină (1)
- Mannheim pair (1)
- Masă imaginară (1)
- Materie condensată (1)
- Matrice (1)
- Mister (1)
- Numere prime (1)
- O lume mai bună (1)
- Paradox (1)
- Particule elementare (1)
- Pas (1)
- Poezii (1)
- Principiul măsurabilității (1)
- Radiație (1)
- Rază complexă (1)
- Serie Fourier (1)
- Simulare (1)
- Tornadă (1)
- Transformări (1)
- Univers (1)
- Viteza de rotație minimă (1)
- Viteză aparentă (1)
- Viteză de scăpare (1)
- Viteză reală (1)
- exponențiala (1)
- matricea Frenet (1)
- publicare (1)
