Torsiunea complexă

​Încă din primii ani de liceu, scumpii ani de liceu, când la mate dai de lucruri extrem de interesante, învăţăm că există un fel de numere minunate numite numere complexe. Printre alte minunăţii de proprietăţi ale acestor numere, aflăm că ele sunt caracterizate de argument, un parametru dependent de raportul dintre partea imaginară a numărului complex şi partea reală a sa, precum şi de modul, un parametru dat de radicalul sumei pătratelor celor două părţi. 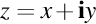Mai precis, dat fiind un număr complex sub forma sa algebrică , argumentul său este 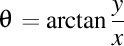, iar modulul acestui număr complex este .

​Această scurtă introducere este suficientă pentru a intra acum în miezul problemei la care vreau să mă refer. Ştim că în Fizica elicoidală şi, mai concret, în teorema de recurenţă a formulelor lui Frenet, apare raportul dintre curbură şi torsiune (raport pe care îl numesc lancretian), precum şi radicalul sumei dintre pătratele curburii şi torsiunii.

​Asociind cele două cunoştinţe, ajungem la concluzia că putem defini o noţiune nouă dacă vom construi un nou număr complex corespunzător fiecărui punct al unei curbe date, astfel încât partea reală a acestui număr complex să fie tocmai torsiunea curbei în acel punct dat, iar partea sa imaginară să fie curbura curbei în punctul respectiv. Numărul complex astfel definit poate fi numit torsiunea complexă a curbei într-un anumit punct. Aşadar, torsiunea complexă poate fi scrisă . 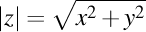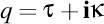Argumentul torsiunii complexe va fi atunci 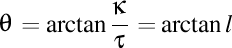, unde am notat cu l lancretianul curbei, iar modulul torsiunii complexe va fi radicalul 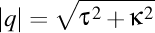. Prin aceasta, putem observa că o curbă a cărei torsiune complexă nu are parte reală este de fapt tocmai o curbă plană, iar o curbă a cărei torsiune complexă nu are parte imaginară este o dreaptă.

​Descoperirea torsiunii complexe ne permite să explorăm în continuare un teren virgin în care putem aplica teoriei curbelor profundele cunoştinţe obţinute de umanitate în domeniul analizei complexe şi putem reformula cu limbajul riguros al acesteia o mulţime de rezultate din teoria curbelor.

​ De exemplu, în baza teoremei fundamentale a curbelor, ştim că orice curbă din spaţiu are forma complet determinată de curbura şi torsiunea ei. Aşadar, în noua formulare, orice curbă are forma complet determinată de un număr complex dat de torsiunea sa complexă. Altfel spus, abstracţie făcând de o rotaţie şi o translaţie, toate curbele cu aceeaşi torsiune complexă sunt identice.

​ Alt exemplu interesant este furnizat de teorema lui Lancret. În noul nostru limbaj al numerelor complexe, teorema lui Lancret ne spune că dacă argumentul torsiunii complexe a unei curbe este constant, atunci curba respectivă este o elice. Aceasta mai înseamnă că dreptele care trec prin origine în planul complex corespund elicelor din spaţiul tridimensional. Şi reciproc. Mai rezultă de aici şi faptul că transformările conforme, adică acelea care păstrează unghiul dintre dreptele planului complex, transformă de fapt elicele în elice, modificând doar modulul torsiunii complexe asociate, nu şi argumentul său.

​ Dat fiind faptul că argumentul torsiunii complexe al unei elice este tocmai unghiul format de tangenta elicei cu axa elicei, apare posibilitatea de a reconsidera definirea reperelor carteziene. Mai precis, putem considera că axa numerelor reale din planul complex este tocmai axa elicelor în spaţiul tridimensional, iar restul dreptelor din planul complex care trec prin originea acestuia sunt elicele care se înşurubează în jurul axei comune.

​Desigur că acest material nu poate constitui altceva decât o poartă modestă deschisă spre o nouă lume minunată a Fizicii elicoidale, lume în care domnesc numerele complexe cu proprietăţile lor remarcabile.