Dacă admitem ca un prim corolar al teoremei rezultatul privind existența vitezei unghiulare minime, atunci putem continua drumul nostru prin această lume inedită a Fizicii teoretice, formulând următorul corolar:
Corolarul 2. În condițiile teoremei de recurenţă a formulelor lui Frenet, dacă există un ordin n pentru care raportul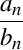 
este constant și nenul, atunci :
-1). raportul de orice ordin mai mare decât n se anulează;
-2). modulul vitezei unghiulare de orice ordin mai mare decât n este egal cu modulul vitezei unghiulare de ordinul n.
Demonstrație.
-1). Avem relația
.
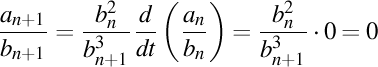Cum orice raport nul este și constant, rezultă că orice raport de ordin mai mare decât n se anulează.
-2). Din relațiile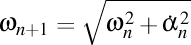 
și
,
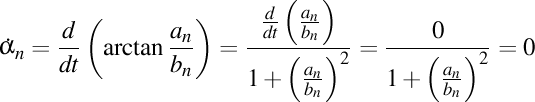rezultă
.
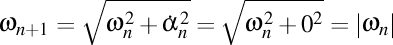Cum orice raport de ordin mai mare decât n este nul, rezultă că toate vitezele unghiulare de ordin mai mare decât n sunt egale în modul.
Având în vedere aceste proprietăți, putem formula următoarea
Definiție. Se numește ordinul caracteristic al mișcării (sau, mai simplu, ordinul mișcării), numărul natural n cu proprietatea că raportul de ordinul n este constant și nenul. Vom spune uneori că un corp se deplasează în ordinul n sau că ordinul (caracteristic al) unui corp este n.
Am speranța că voi reuși să vă prezint o legătură între viteza unghiulară minimă și sarcina electrică a electronului, precum și o legătură între cuantificarea energiei și cuantificarea manifestată în aceste proprietăți ale mișcării.
Niciun comentariu:
Trimiteți un comentariu
Comentariile vor fi moderate în măsura timpului meu disponibil, după care vor apărea pe blog. Voi încerca să public doar comentariile consistente sau interesante sau adevărate sau corecte sau la obiect. Voi căuta să le elimin pe cele din care nu avem nimic de învățat sau pe cele care afectează negativ mintea cititorului sau reclamele fără legătură cu blogul. De asemenea, voi face tot posibilul să răspund la comentariile care cer un răspuns. Vă mulţumesc pentru efortul vostru de a scrie în lumina acestor consideraţii!