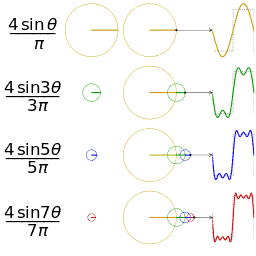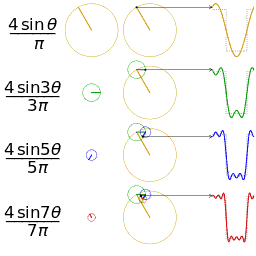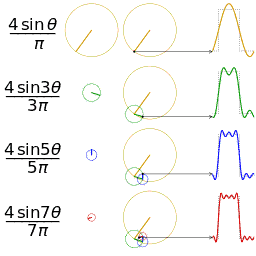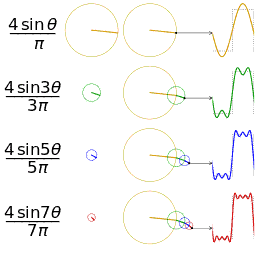Paradoxul informațional al mișcării rectilinii

Se știe (https://en.wikipedia.org/wiki/Quantum_no-deleting_theorem, http://van.physics.illinois.edu/qa/listing.php?id=24045 ) că informația conținută într-un sistem nu poate fi nici creată, nici distrusă. 

Așadar, dacă un corp se deplasează pe o anumită traiectorie, informațiile despre curbura și torsiunea traiectoriei respective ar trebui să se conserve, indiferent de transformările suferite de corpul respectiv.

Să presupunem atunci pentru început că, sub influența unor forțe, un corp se deplasează întâi pe o traiectorie a cărei curbură și torsiune sunt nenule și bine determinate, stare pe care o numim „stare inițială”. 

Apoi, în urma unui proces oarecare (de exemplu, eliberarea corpului de forțe), corpul începe să se miște rectiliniu, adică pe o linie dreaptă, stare pe care o numim „starea finală”. Linia dreaptă are curbura nulă, iar anularea curburii ar putea fi corelată informațional cu intensitatea forțelor care au produs starea inițială. 

Problema este, însă, TORSIUNEA. Torsiunea dreptei este imposibil de determinat (https://en.wikipedia.org/wiki/Frenet%E2%80%93Serret_formulas#Special_cases).  Așadar, informația despre torsiunea din starea inițială se pierde iremediabil în starea finală! Dar acest lucru contravine principiului conservării informației.

Desigur, problema se poate și inversa. Se poate considera că în starea inițială corpul se deplasează rectiliniu, după care, în starea finală, începe să se deplaseze pe o curbă cu torsiunea bine definită. În acest caz, informația ar fi creată din nimic, fapt care din nou contrazice principiul conservării informației.

Cum se rezolvă problema? Propunerea mea este Fizica elicoidală, o Fizică în care MIȘCAREA RECTILINIE ESTE IMPOSIBILĂ.

Fizica elicoidală este precum geometriile neeuclidiene

Geometria neeuclidiană diferă de geometria euclidiană printr-un singur postulat: postulatul paralelelor. Mai exact, în timp ce geometria euclidiană spune că „printr-un punct exterior unei drepte putem duce o singură paralelă la acea dreaptă”, geometriile neeuclidiene neagă această propoziție. Și fiecare negație posibilă duce la o geometrie nouă posibilă: dacă admitem că printr-un punct exterior unei drepte nu putem duce nici o dreaptă paralelă la acea dreaptă, obținem geometria eliptică, iar dacă admitem că prin acel punct putem duce mai multe (o infinitate de) drepte paralele cu dreapta dată, obținem geometria hiperbolică. Dar cel mai important este că (prin anularea unui parametru) din geometriile neeuclidiene REZULTĂ geometria euclidiană, dar nu și invers!

Tot astfel, în Fizica elicoidală, postulatul care face diferența este postulatul inerției. Fizica actuală spune că un corp liber se deplasează pe o linie dreaptă, pe când Fizica elicoidală neagă această propoziție. Negația acestei propoziții duce spre o curbă care, spre deosebire de dreaptă, are curbură și torsiune nenule (și constante într-un mediu uniform). Așadar, negația ne duce spre elicea circulară. Apoi, dacă anulăm curbura acestei elice din Fizica elicoidală, obținem Fizica actuală.

Democrația prin Internet

Democrația reprezentativă, bazată pe alegeri, a eșuat, prin corupție. Am tot avut până acum alegeri peste alegeri. Nu vreau să mai aud de acest cuvânt! Alegerile anticipate nu sunt o soluție. Ele nu fac decât să propage în continuare sistemul corupt. Niciun om ajuns acolo sus nu mai poate fi onest, pentru că este ori mituit, ori amenințat.

De-acum singurul lucru în care mai am încredere este votul DIRECT al Poporului, prin internet. Poporul să propună legile direct pe internet, el să le voteze, el să le pună în aplicare. Nu mai este nevoie de Parlament. Parlamentul trebuia într-o societate în care nu exista internetul. Dar de-acum nu mai avem nevoie de porcăria asta numită „Parlament”.

Care-i treaba cu Eminescu?

Din lecturile tinereților mele am aflat că Eminescu ar fi murit de tot felul de boli ciudate. Însă n-am citit nimic ceva argumentat atât de clar despre el. Așa că materialul următor m-a pus pe gânduri. Și tare mă tem că nici astăzi nu stăm mai bine la capitolul „libertate”.

http://gandeste.org/general/adevarul-despre-cum-a-murit-mihail-eminescu-ucis-la-comanda/37025

Centrul Universului și antimateria

Toate sistemele fizice au un centru de masă, centru în care sau din care se presupune (în Fizica elicoidală) că pleacă toate celelalte corpuri ale sistemului respectiv. Corpurile sistemului parcurg elice închise, care au originea în centrul de masă.

În Fizica elicoidală, prin definiție, corpurile nu mai ating niciodată centrul, căci drumul ce trebuie parcurs până la centru este infinit de lung, căci acest drum este cu atât mai întortocheat, cu cât este mai aproape de centru. Altfel spus, centrul sistemului se mișcă pe cea mai întortocheată traiectorie posibilă și de aceea are lancretianul mediu infinit.

Corpurile care se îndepărtează de centru sunt materie, iar corpurile care se apropie de centru sunt antimaterie. Sau invers?

Viteză medie și lancretian mediu

Un corp care se deplasează pe o elice are viteza medie mai mică decât viteza cu care se deplasează el efectiv pe elice. Pentru că degeaba are el sute de kilometri pe oră de-a lungul elicei, din moment ce elicea are spire multe și corpul aproape că nu înaintează deloc.

Avem o formulă pentru viteza medie, în funcție de parametrii elicei. Dacă elicea are curbura $\kappa$ și torsiunea $\tau$, iar corpul se deplasează de-a lungul elicei cu viteza $c$, atunci viteza medie pe care o are corpul este 

$$v=\frac{c}{\sqrt{1+l^2}}.$$

Am notat cu $l=\frac{\kappa}{\tau}$ raportul dintre curbură și torsiune, adică „lancretianul” elicei.

Dacă un corp se deplasează cu viteza $c$ pe o traiectorie mult mai întortocheată decât elicea și are viteza medie $v$, atunci putem vorbi de un lancretian mediu, care rezultă din aplicarea formulei de mai sus. Adică, avem

$$l=\sqrt{\frac{c^2}{v^2}-1}.$$ 

Descompunerea Fourier seamănă cu descompunerea în elice

Se știe că seriile Fourier ne permit să descompunem aproape orice funcție în funcții sinusoidale. Acest lucru este valabil pentru funcții cu graficul în plan.

Tot astfel, teorema de recurență a formulelor lui Frenet ne spune că aproape orice curbă din spațiu (deci, grafic în spațiu) se descompune în elice elementare.

Câmp și substanță

În concepția mea, în lume există o mulțime discretă (numărabilă) de particule cu masă nenulă (substanța) și o mulțime continuă (nenumărabilă) de particule cu masă nulă (câmpul).

Deci, într-un volum finit există un număr finit de particule de masă nenulă și un număr infinit de particule de masă nulă.

Particulele de masă nenulă se deplasează cu viteză mai mică decât a luminii, iar particulele de masă nulă se deplasează cu viteza luminii.

Masa unui volum finit ocupat de substanță este produsul dintre numărul finit de particule aflate în acel volum și masa nenulă particulelor respective (presupuse identice în volumul ales). Masa este în acest caz o sumă.

Masa unui volum ocupat de câmp este dată de produsul dintre numărul infinit de particule aflate în acel volum și masa nulă a particulelor respective. Masa este în acest caz o integrală.

În ultimă instanță, substanța poate fi considerată un câmp foarte dens, iar câmpul poate fi considerat o substanță foarte rarefiată. Orice abordare unilaterală a vreunei laturi a acestei dihotomii trebuie să fie echivalentă cu cealaltă, atât din punct de vedere matematic, cât și fizic.

Cum vi se pare democraţia directă din Elveţia?

Am aflat abia recent (pe Facebook) că în Elveția funcționează un fel de democrație directă, mult mai eficientă decât restul bătăilor de joc numite „democrații”. Nu cumva Elveția o duce așa bine din cauza acestei democrații?

Satelitul unui număr complex

În pregătirea aparatului matematic pe care îl voi utiliza la elaborarea Fizicii elicoidale, introduc aici noțiunea de „satelit al unui număr complex”. 

Definiție. Fie funcțiile de parametrul $t$, $a=a(t)$ și $b=b(t)$. Atunci, numim satelit al unui număr complex dat sub forma algebrică $z=z(t)=a+bi$, numărul complex $$z(t)^{\circ}=c+di,$$ unde $$c=c(t)=\frac{l^\prime}{1+l^2},$$ iar $$d=d(t)=\sqrt{a^2+b^2}.$$ Aici am notat cu $l=l(t)=\frac{b}{a}$ așa-numitul lancretian al numărului complex $z$. De asemenea, putem numi darbuzianul lui $z$ modulul $d=d(t)=\sqrt{a^2+b^2}$ al numărului complex $z$.

Definiția este inspirată din faptul că traiectoriile sateliților planetelor sunt guvernate de sateliții numerelor complexe asociate traiectoriilor planetelor.

Am creat o petiție

Din dragoste pentru toți oamenii, am creat o petiție. Cu cât va fi conștientizată de cât mai mulți oameni, cu atât se vor deschide noi orizonturi pentru îmbunătățirea nivelului nostru de trai, al tuturor. Votați cu inimă deschisă și cu speranța că se va realiza.

Ea are următorul conținut:


„Votați pentru limitarea discrepanței nesimțite dintre bogați și săraci.

Se știe că în prezent nu există o lege care să limiteze superior bogăția. Oricine poate fi oricât de bogat, teoretic, infinit de bogat. Și chiar există oameni atât de bogați încât sunt nevoiți să-și miște banii în hambare cu buldozerul, pentru ca aceștia să nu le mucegăiască. Dar acest lucru are consecințe dezastruoase. Omul bogat poate cumpăra aproape orice. Din păcate, el îi poate cumpăra chiar și pe cei care trebuie să apere legea. Astfel, omul extrem de bogat poate face oricâte lucruri ilegale, căci el poate corupe sau amenința aproape orice om, subjugându-l.

Acum, imaginați-vă că niciun om nu ar putea fi atât de bogat încât să-l cumpere pe alt om. În aceste condiții, nu ar mai exista corupție. Atunci, toate visurile noastre nu ar mai fi îndreptate înspre înavuțire materială, ci înspre înavuțire spirituală, o avere pe care nu ți-o poate manipula nimeni, nu ți-o poate da fără efort nimeni și nici nu ți-o poate lua. Într-o asemenea lume nu ar mai exista oameni care să doarmă pe străzi, nu ar mai exista cerșetori, nu ar mai exista copii flămânzi. Într-o asemenea lume, nivelul de trai nu ar mai putea coborî niciodată, deoarece toți membrii societății ar avea un obiectiv comun: îmbogățirea simultană a oamenilor. Astfel, toată tehnologia noastră, toată cunoașterea noastră, pe care am dobândit-o cu trudă de-a lungul istoriei, s-ar reflecta în creșterea inevitabilă a nivelului de trai al fiecărui cetățean, așa cum e și firesc.

Nu este firesc să existe oameni care nu au muncit nici o zi în viața lor și să-și permită luxul de a călători oriunde în lume. Nu este firesc ca oameni care s-au născut în pielea goală pe această planetă să aibă câștiguri de milioane de euro în timp ce dorm. Nu este firesc să primești mai mult de la societate decât i-ai dat acesteia înapoi. Te-ai născut în pielea goală, niște părinți produși de societate te-au educat și ți-au dat să mănânci, apoi o școală te-a învățat lucruri minunate pe care le-au aflat cu mare trudă și pasiune predecesorii tăi. Așa că nu-ți imagina că poți fi de miliarde de ori mai bogat decât un biet cerșetor care își duce veacul într-o peșteră.

Societate tocmai asta înseamnă: colaborare. Nu junglă. Numai în junglă discrepanța este dată de forța brută. De ce să permitem să existe în societate forță brută, forța banului? Banii, însemnând valoare obținută în comun de societate, trebuie să fie împărțiți frățește între toți membrii societății. Dacă ai ales să trăiești în societate (și bine ai făcut), atunci trebuie să împarți și bunele și relele cu alții.

Într-adevăr, în societate există și oameni leneși. Dar ei sunt niște handicapați, niște oameni bolnavi, iar bolnavii trebuie ajutați. Ei sunt produsul societății, iar societatea trebuie să-și plătească greșelile. Plătindu-și greșelile, va învăța să evite lenea și să-i ajute pe cei care nu știu mai mult decât să fie leneși. Copilul nu se naște leneș, așa că undeva pe parcurs, unii nu sunt învățați cum se cuvine și își pierd apetitul pentru viață. Vom găsi soluții și la această problemă. Dar ea nu trebuie să ne împiedice în drumul nostru pentru realizarea acestui vis minunat: împărțirea frățească a bogățiilor.

Așadar, consider că cea mai valoroasă decizie posibilă pentru o lume mai bună este abolirea discrepanţei dintre bogaţi şi săraci. Prin această abolire înţeleg uniformizarea veniturilor de orice fel, astfel încât cel mai bogat om din lume să nu poată avea o avere mai mare de n-ori decât cel mai sărac om din lume, unde n să fie un număr natural (numit „discrepanţă”) din ce în ce mai mic şi mai apropiat de unitate. Cu cât discrepanţa unei societăţi va fi mai mică, cu atât societatea respectivă va fi mai evoluată, atât material, cât mai ales spiritual.

Am putea începe cu o discrepanță de n=10. Asta ar însemna că cel mai bogat om din lume să fie cel mult de 10 ori mai bogat decât cel mai sărac om din lume. Apoi, în deceniul următor, discrepanța să fie n=9, apoi, peste 20 de ani, discrepanța să fie n=8 și așa mai departe.

Este important să nu confundați lumea propusă de mine cu comunismul. În comunism nu era limitată superior bogăția, căci boșii de sus puteau avea oricâte. Noi vrem o LEGE clară, în care să fie stipulată discrepanța maximă admisă între un bogat și un sărac. Noi vrem să știm că nivelul de trai al omenirii se împarte frățește la toți membrii societății.

Așadar, votați această petiție. Ea vă va rezolva indirect și alte probleme care se cer a fi rezolvate.

Vă mulțumesc pentru atenție!

Cu drag, al vostru Abel”

Teorema de recurență a fost descoperită deja înaintea mea

Am primit în seara asta un email de la la domnul Vladimir Volenec prin care îmi semnalează faptul că teorema de recurență este deja prezentă în lucrări mai vechi, precum http://books.google.ro/books?id=8tgmFQ6EPTIC&pg=PA129&redir_esc=y#v=onepage&q&f=false

Bucuria pe care mi-a creat-o vreau s-o împărtășesc și cu voi. Sunt bucuros că într-o lume ce părea pustie, a apărut o luminiță ce-mi dă speranța că nu voi rămâne neînțeles și că mai există pasionați ca mine de domeniu.

Noțiunea de elicor

Prin analogie cu noțiunea de vector, vom introduce aici noțiunea de elicor.

Elicorul este o porțiune elementară a unei elice circulare determinată de un pas al acesteia, deci o spiră a elicei, pe care s-a stabilit un sens de parcurs. Astfel, elicorul are următoarele proprietăți:

• Origine. Este punctul din care pornește elicorul.
• Extremitate. Este punctul în care se termină elicorul.
• Direcție. Este axa elicei circulare ce definește elicorul.
• Sens. Sensul în care se ajunge din origine în extremitate.
• Rază. Este raza elicei circulare ce definește elicorul.
• Pas. Este pasul elicei circulare ce definește elicorul.
• Lungime. Este lungimea porțiunii de elice circulară ce definește elicorul.

Observați că elicorul generalizează noțiunea de vector, în sensul că vectorul este un elicor a cărui rază este nulă.

Probleme cu principiul actual al inerției

Să ne imaginăm următorul experiment. O bilă se deplasează cu viteză constantă prin spațiu. La un moment dat, bila începe să emită două fluxuri luminoase în direcții opuse și perpendiculare pe viteză. Prin acest mecanism, bila pierde masă. 

Dar asupra ei nu acționează nicio forță, din moment ce fluxurile luminoase sunt emise în direcții opuse. Așadar, dacă asupra bilei nu acționează forță, atunci impulsul ei trebuie să rămână constant.

Dar am văzut că masa bilei scade, din moment ce ea emite fluxuri luminoase. Și cum impulsul ei trebuie să rămână constant, rezultă că va trebui să crească viteza ei, pentru a compensa scăderea masei.

Dar, principiul actual al inerției ne spune că un corp asupra căruia nu acționează forțe își menține starea de mișcare rectilinie și uniformă.

Cum se împacă aceste lucruri?

Precizări pentru principiul elicoidal al inerției

Știți deja că, spre deosebire de Fizica actuală, în Fizica elicoidală este valabil următorul principiu al inerției:

-un corp liber se mișcă pe o elice circulară (deci, nu pe o dreaptă).

Acum sunt în măsură să aduc precizări suplimentare, cantitative, în legătură cu acest principiu. Astfel, principiul elicoidal al inerției poate fi formulat și mai precis în modul următor:

Un corp liber care se mișcă într-un mediu omogen descrie o elice circulară, al cărei lancretian este dictat de mediu, iar al cărei darbuzian este dictat de corp. Lancretianul depinde de indicele de refracție al mediului, iar darbuzianul depinde de masa corpului.

Reamintesc aici că lancretianul este raportul dintre curbură și torsiune, iar darbuzianul este modulul vectorului lui Darboux. Adică, lancretianul este $$l=\frac{\kappa}{\tau}$$ și darbuzianul este $$d=\sqrt{\kappa^2+\tau^2}.$$

Torsiunea de ordin superior este dată de precesia darbuzorilor

Observați că teorema spune că torsiunea de ordin superior este dată de $\tau_{n+1}=\sqrt{\dot\theta_n^2+\dot\theta_{n-1}^2+\dots+\dot\theta_1^2+\tau^2}$, unde $\tau$ este torsiunea de ordinul cel mai mic, torsiunea fundamentală, care este, probabil, o constantă universală. Aici, unghiurile $\theta_i$ cu indicele de la 1 la n sunt unghiurile cu care precesează darbuzorii respectivi.

De exemplu, pentru elice, toți darbuzorii sunt constanți, deci unghiul de precesie este nul. Pentru curba de precesie constantă (care este o elice de ordinul doi), darbuzorul de ordinul unu variază, dar sunt constanți toți ceilalți darbuzori. Și așa mai departe.

Mai observați că radicalul ce semnifică torsiunea poate fi considerat un fel de „distanță” într-un spațiu n-dimensional.

Interferența ar putea fi explicată și cu teoria corpusculară

Dacă am admite că lumina este alcătuită din corpusculi care se deplasează elicoidal, atunci am putea explica interferența luminii prin faptul că doi corpusculi apropiați ar putea interacționa în modul următor:

Puteți observa din aceste desene că mișcarea elicoidală a particulelor are posibilități mult mai mari pentru explicarea lumii.

Avem o prejudecată fabricată față de sistemul egalitarist?

Tare mă tem că niște capitaliști putred de bogați, care își vântură banii cu buldozerul ca să nu mucegăiască, au reușit să inoculeze și să întrețină prejudecata că sistemul comunist ar fi utopic. Au inițiat această acțiune atunci când și-au dat seama că un sistem bazat pe egalitate ar pune în pericol averile lor fabuloase. Asta i-a determinat să se unească într-o societate secretă ce influențează lumea.

Și chiar mă gândesc că falimentul comunismului a fost stimulat din exterior de asemenea oameni bogați și organizați, care au reușit să corupă sau să înșele oamenii influenți din fruntea fostelor societăți comuniste într-atât încât să producă impresia cetățenilor că egalitatea este utopică și ar duce la dezastre.

Mai cred că sărăcia de pe vremea lui Ceaușescu a fost planificată de către aceștia ca să-i determine pe cetățeni să urască tot ce ține de comunism. Și mai cred că în Coreea de Nord se menține voit această stare pentru a arăta lumii că, chipurile, comunismul, egalitarismul este inuman.

Dar, dimpotrivă, inumană este societatea capitalistă, care nu diferă prin nimic de junglă. Societatea umană ar trebui să progreseze cu fiecare an în care se fac descoperiri tehnologice, iar acest progres trebuie să se reflecte fără excepție în bunăstarea fiecărui cetățean, indiferent de capacitățile acestuia, indiferent de handicapurile sale.

Dragii mei cititori, meditați la aceste lucruri! Nu vă lăsați păcăliți de prejudecata că egalitarismul ar fi utopic. Nu este utopic. Egalitatea financiară (sau măcar limitarea discrepanței dintre bogați și săraci) dintre oameni trebuie stipulată prin lege. Nimeni nu are voie să fie mai bogat decât altul în societate, căci nimeni nu am adus cu noi bogăția din altă lume când ne-am născut. Tot ceea ce am realizat pe Pământ, am realizat datorită semenilor noștri. Niciunul dintre noi nu suntem mai cu coarne ca să avem atât de mult în raport cu alții încât noi să ne vânturăm banii cu buldozerul, iar alții să se spetească muncind doar pentru a plăti rate la bancă.

Soluția este dată de următoarele etape:

• informarea corectă a tuturor oamenilor de bine privind posibilitățile egalitarismului;
• organizarea acestor oameni de bine într-o societate pregătită să înfrunte jungla ce domnește azi în lume;
• conceperea și redactarea unei legi egalitariste;
• promulgarea și aplicarea legii.

Toate necazurile societății noastre provin din faptul că trăim încă într-o junglă în care unii vor și reușesc să aibă mai mult, pe spinarea celor corecți și tăcuți care continuă să muncească sperând că odată și odată le va fi mai bine și lor.

Electronul, un foton încărcat?

Am primit acest linc de la un prieten:

http://www.researchgate.net/publication/267922850_The_Electron_Is_a_Charged_Photon

Autorul acestui articol parcă descoperă rolul elicei în mecanica cuantică. S-o țină tot așa!

Metrici elicoidale

Să presupunem o curbă a cărei curbură este o funcție de timp $\kappa=\kappa(t)$. Conform teoremei lui Taylor, putem descompune această funcție de curbură în serie de puteri și putem neglija termenii de ordin mare.

Dacă neglijăm toți termenii de ordin superior și admitem că curbura este nulă, suntem în cazul metricii euclidiene.

Dacă neglijăm toți termenii de ordin superior dar admitem că curbura este constantă și nenulă (deci prima derivată a curburii este nulă), suntem în cazul unei metrici elicoidale (de ordinul unu).

Dacă neglijăm toți termenii de ordin superior dar admitem că prima derivată a curburii este constantă și nenulă (deci a doua derivată a curburii este nulă), suntem în cazul unei metrici elicoidale (de ordinul doi).

Dacă neglijăm toți termenii de ordin superior dar admitem că a doua derivată a curburii este constantă și nenulă (deci a treia derivată a curburii este nulă), suntem în cazul unei metrici elicoidale (de ordinul trei).

Și așa mai departe...

Cum ar fi dacă s-ar reconstrui teoria relativității generalizate pe această bază? Nu cumva s-ar strecura apoi aici și elemente din Fizica cuantică?

Teorema de recurență a fost publicată

Am bucuria să vă anunț apariția articolului meu privind teorema de recurență a formulelor lui Frenet într-o revistă peer review: https://www.creative-mathematics.cunbm.utcluj.ro/article/the-recurrence-theorem-of-frenet-formulae/

Deoarece nu am plătit pentru Open Access, acolo găsiți abstractul articolului. Dar, în esență, acolo prezint demonstrația teoremei, precum și o serie de consecințe, printre care și elicea generalizată de ordinul n.

Oare chiar nu există sistem de referință absolut?

Ciudată întrebare! Am început să pun la îndoială răspunsul negativ pe care îl dă Știința actuală acestei probleme. Și iată de ce.

Să urmăm îndeaproape faptele. Totul a pornit de la Galilei. Acesta a făcut experimentele lui rudimentare (unele chiar imaginare) și a concluzionat că un observator de pe o corabie, de exemplu, aflată departe de țărm pe un ocean liniștit, nu va putea ști cu ce viteză se deplasează față de malurile oceanului. Ba, mai mult, nici nu va putea ști dacă se deplasează ori ba, din moment ce muștele nu se adună la urma corabiei, iar experimentele făcute pe corabie nu scot în evidență niciun fel de mișcare exterioară.

Noi știm astăzi, însă, că rotația Pământului implică forțe care permit determinarea mișcării acestuia, ceea ce îl face un sistem de referință neinerțial. Așa că, pentru o precizie și mai mare, alegem un sistem de referință legat solidar cu Soarele. Apoi știm că și Soarele se mișcă accelerat în jurul centrului Galaxiei, așa că un sistem de referință și mai precis ar fi unul legat solidar cu Galaxia.

Dar, dacă mergem așa mai departe? Dacă și Galaxia face parte dintr-un alt sistem pe care îl putem considera un sistem de referință inerțial mai bun? Dar, dacă mergem și mai departe? Nu cumva am putea să ajungem la un sistem de referință „maxim”, pe care să-l putem considera sistemul de referință absolut?