Theorem: If there is a right trihedron of the n order
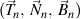
that satisfies the Frenet formulas of the n order, written in the trigonometric form
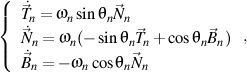
then there is still a right trihedron of the n+1 order
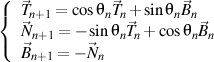
that satisfying, in turn, the Frenet formulas of the n+1 order written also in the trigonometric form
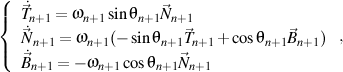
where
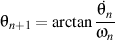 and
and 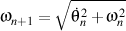
.
Demonstration: Through relations
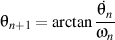 and
and 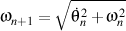
we have that
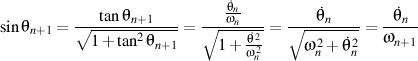
so
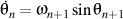
.
We also have
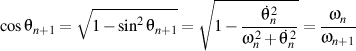
whence
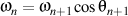
.
Now, we derive the unit vectors of the trihedron of the n+1 order
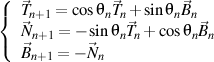
and we obtain
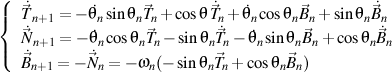
.
Replacing
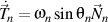 and
and
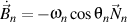
, we obtain
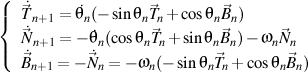
.
But, from the definition of the unit vectors of the high order, we know that
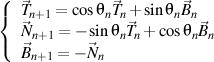
,
so
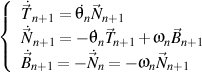
.
Because
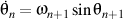 and
and 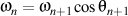 ,
,finally result that
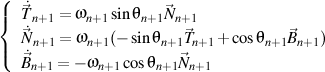
,
qed.

Niciun comentariu:
Trimiteți un comentariu
Comentariile vor fi moderate în măsura timpului meu disponibil, după care vor apărea pe blog. Voi încerca să public doar comentariile consistente sau interesante sau adevărate sau corecte sau la obiect. Voi căuta să le elimin pe cele din care nu avem nimic de învățat sau pe cele care afectează negativ mintea cititorului sau reclamele fără legătură cu blogul. De asemenea, voi face tot posibilul să răspund la comentariile care cer un răspuns. Vă mulţumesc pentru efortul vostru de a scrie în lumina acestor consideraţii!