Théorème: s'il ya un trièdre droit de n ordre
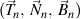
qui satisfait les formules de Frenet de n ordre, écrite comme la forme trigonométrique
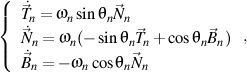
alors il ya un trièdre droit de n+1 ordre
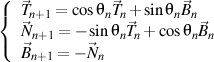
qui satisfait, à son tour, les formules de Frenet de n+1 ordre, écrite aussi comme la forme trigonométrique
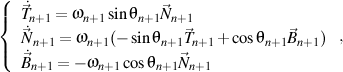
où
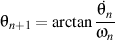 et
et 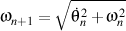
.
Démonstration :
Grâce à des relations
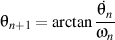 et
et 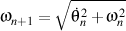
nous avons que
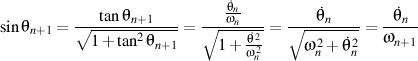
si
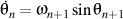
.
Nous avons également
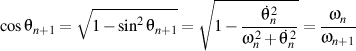
d'où
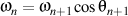
.
Maintenant, nous dérivons les vecteurs unitaires du trièdre de l'ordre n +1
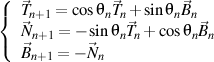
et nous obtenons
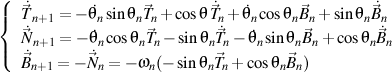
.
Remplacer
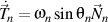
et
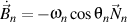
, nous obtenons
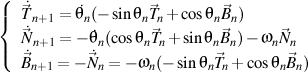
.
Mais, d'après de la définition des vecteurs unitaires de l'ordre de haut, nous savons que
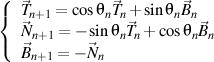
,
si
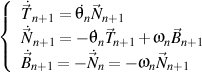
.
Parce que
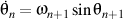 et
et 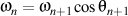 ,
,finalement abouti
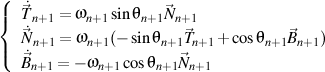
,
ce qui devrait être démontré.

Niciun comentariu:
Trimiteți un comentariu
Comentariile vor fi moderate în măsura timpului meu disponibil, după care vor apărea pe blog. Voi încerca să public doar comentariile consistente sau interesante sau adevărate sau corecte sau la obiect. Voi căuta să le elimin pe cele din care nu avem nimic de învățat sau pe cele care afectează negativ mintea cititorului sau reclamele fără legătură cu blogul. De asemenea, voi face tot posibilul să răspund la comentariile care cer un răspuns. Vă mulţumesc pentru efortul vostru de a scrie în lumina acestor consideraţii!