Am „descoperit” ieri o aplicaţie gratuită numită „Zim” despre care am constatat că are o mulţime de caracteristici interesante:
- poate fi folosită pe sistemele de operare Windows, Linux şi Mac;
- salvează automat toate modificările aduse în fişiere text ce pot fi editate ulterior cu alt program preferat;
- are o interfaţă care permite vizualizarea dintr-o privire atât a paginilor spre care face trimitere pagina curentă, cât şi a celor care fac trimitere la ea, precum şi a indexului şi a tagurilor recent utilizate;
- admite o largă paletă de formatări şi de module, precum este cel pentru ecuaţii matematice scrise în LaTeX;
- permite inserarea de imagini şi de ataşamente;
- are facilităţi de automatizare a creării legăturilor, prin scurtături de tastatură ce fac minuni, legături ce pot fi vizualizate în imagini asemănătoare hărţilor mentale.
Vă recomand cu căldură să folosiţi această aplicaţie simplă şi gratuită toţi cei care visaţi la un sistem wiki direct pe calculatorul vostru.
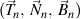
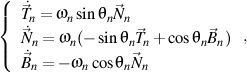
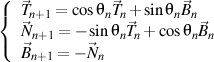
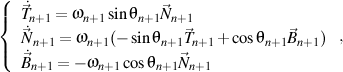
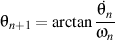 et
et 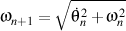
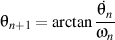 et
et 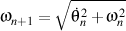
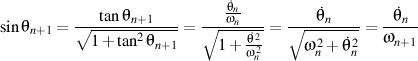
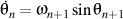
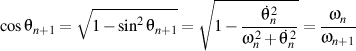
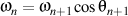
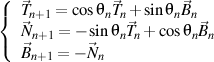
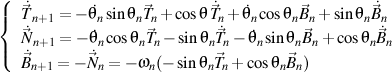
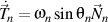
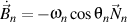
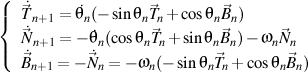
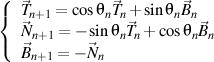
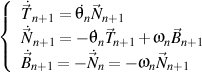
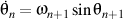 et
et 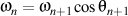 ,
,