Se numeşte serie Fourier o funcţie ce poate fi scrisă sub forma
,
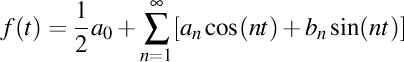unde
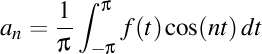
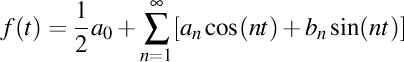,unde
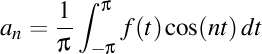
şi
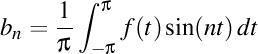
sunt nişte coeficienţi care depind numai de n.
Vrem să determinăm primele derivate ale unei asemenea funcţii şi să analizăm dacă aceste derivate se pot scrie una în funcţie de cealaltă.
Vrem să determinăm primele derivate ale unei asemenea funcţii şi să analizăm dacă aceste derivate se pot scrie una în funcţie de cealaltă.
Având în vedere faptul că toţi coeficienţii seriei Fourier sunt independenţi de parametrul t, prima derivată a seriei Fourier este
.
.
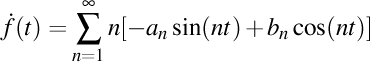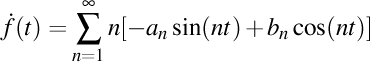Dacă mai derivăm o dată prima derivată, obţinem că a doua derivată este
.
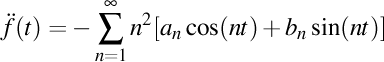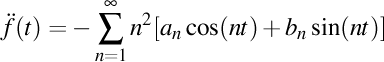. Oare există vreo legătură între seria Fourier şi cea de-a doua sa derivată? Observăm că în ambele apare expresia
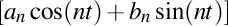. Dar se pare că asta nu este suficient pentru a putea găsi o legătură mai adâncă între derivate.
Problema este că ne încurcă apariţia unei puteri din ce în ce mai mari a lui n, fenomen ce
complică mult derivatele de ordin superior şi spulberă speranţa mea de a
găsi o recurenţă printre derivatele seriilor Fourier.
Aşa că mai rămâne să
analizăm dacă se poate găsi o formă simplă pentru curbura şi torsiunea
unei curbe închise, deci definite de serii Fourier.
Niciun comentariu:
Trimiteți un comentariu
Comentariile vor fi moderate în măsura timpului meu disponibil, după care vor apărea pe blog. Voi încerca să public doar comentariile consistente sau interesante sau adevărate sau corecte sau la obiect. Voi căuta să le elimin pe cele din care nu avem nimic de învățat sau pe cele care afectează negativ mintea cititorului sau reclamele fără legătură cu blogul. De asemenea, voi face tot posibilul să răspund la comentariile care cer un răspuns. Vă mulţumesc pentru efortul vostru de a scrie în lumina acestor consideraţii!