Să presupunem că în Univers există un inel omogen foarte subţire cu raza de repaus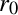 
şi masa de repaus 
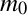. Mai presupunem că un observator aflat în repaus faţă de centrul inelului constată că inelul se roteşte cu o viteză periferică de modul v. În acest caz, modulul momentului cinetic al inelului va fi dat de relaţia J=mvr, unde m este masa de mişcare a inelului faţă de observatorul aflat în centrul inelului, iar r este raza inelului aflat în mişcare pe care o măsoară observatorul din centrul inelului.
Aşa cum am arătat în materialul despre paradoxul lui Ehrenfest, masa inelului aflat în mişcare de rotaţie este mai mare decât masa inelului aflat în repaus, iar raza inelului aflat în mişcare de rotaţie este mai mică decât raza inelului aflat în repaus, aşa cum reiese din formulele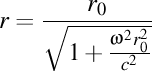 
şi, respectiv,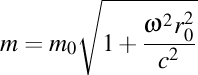
.
Din aceste două relaţii minunate observaţi acum, mai ales, faptul că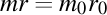 
, adică produsul dintre masă şi rază este un invariant relativist, chiar şi în mişcarea de rotaţie, nu doar în cea de translaţie. De aici mai rezultă că masa de mişcare a unui inel este invers proporţională cu raza inelului, căci 
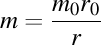. Această ultimă constatare ne permite să concluzionăm de asemenea faptul că momentul cinetic al unui inel subţire este direct proporţional cu viteza periferică cu care se roteşte inelul, conform relaţiei 
.
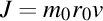Dar, în materialul citat am arătat că momentul cinetic al unui inel este dat de formula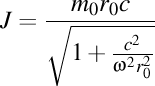
.
Cum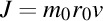 
, rezultă relaţia foarte interesantă
,
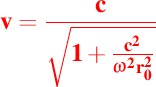relaţie care ne furnizează o legătură relativistă între viteza periferică, viteza de rotaţie şi raza de repaus a inelului. Observaţi că viteza periferică a unui inel nu poate depăşi viteza luminii în vid, chiar dacă viteza unghiulară a inelului este infinită! Desigur, asemenea relaţii relativiste sunt importante mai ales pentru inele cu viteze periferice foarte mari, cum intervin în cazul particulelor elementare, care au viteze de rotaţie foarte mari, cât şi în cazul inelelor cu raze de repaus foarte mari, cum intervin în cazul sistemelor astronomice. Neglijarea relaţiilor relativiste pentru sistemele astronomice foarte mari sau aflate în rotaţie foarte rapidă precum sunt galaxiile sau corpurile foarte dense împiedică înţelegerea clară a fenomenelor cosmice.
Dacă m=m0r0/r, se poate considera că atunci când m tinde la infinit iar r tinde către zero inelul se transformă într-o singularitate?
RăspundețiȘtergereDa, din punct de vedere teoretic, ar fi vorba de o singularitate, dar nu cred că asta se întâmplă şi din punct de vedere fizic. Ceva interzice ca masa să devină infinită sau raza să se anuleze.
RăspundețiȘtergereEu vad spatiul ca fiind o singura dimensiune, a doua fiind energia, si a treia timpul.
RăspundețiȘtergereSpatiul si energia formeaza un plan pe care axa timpului e perpendiculara.
Problema e ca daca vedem lucrurile astfel, transformarea Lorentz (asa cum o arata si numele) poate transforma valori aflate in acelas plan. Cum axa timpului are valoarea zero in planul format de spatiu si energie,introducerea valorilor dependente de timp duce la nedeterminare, de unde si imposibilitatea transformarii inelului intr-o singularitate.
Deci transformarile Lorentz pot fi utilizate pentru transformarea valorilor dintr-o dimensiune, relativ la una singura din celelalte doua.
Aici sta si eroarea teoriei relativitatii, care nu este gresita, dar se intinde mai mult decit e posibil.
Voi fi mai explicit intr-o postare pe forum. As putea deschide un topic despre spatiul negativ ?
Interesantă propunerea ta cu timpul perpendicular pe spaţiu şi pe energie. Dar nu uita că până nu găseşti justificarea acestei propuneri ea pare să nu aibă nicio valoare intrinsecă.
ȘtergereDesigur că poţi deschide un topic despre spaţiul negativ.