Fie două şiruri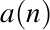 
şi 
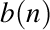de numere naturale, precum şi un şir 
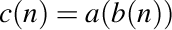dat de compunerea celor două şiruri. Se pune problema de a stabili o formulă pentru coborâtul şirului compus 
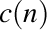în funcţie de coborâtele şirurilor 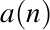şi 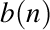. În materialul despre calculul descendent şi ascendent am definit coborâtul unui şir 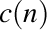ca fiind şirul dat de diferenţa a doi termeni consecutivi ai şirului dat, adică 
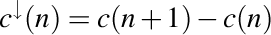. Atunci, pentru a defini în mod consecvent coborâtul unui şir compus, să observăm că definiţia coborâtului unui şir o putem scrie şi în modul următor
.
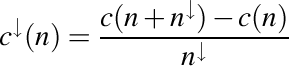În acest context, prin generalizare, putem să convenim că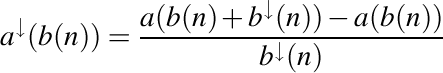
.
Cu aceasta, având în vedere faptul că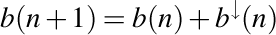 
, putem scrie formula coborâtului unui şir compus ca fiind dată de
.
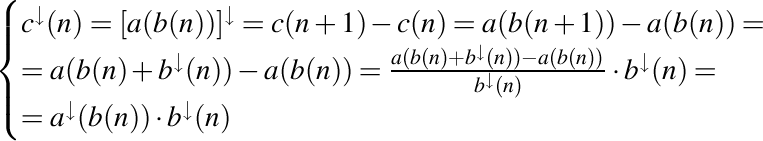Observaţi din nou cu această ocazie analogia profundă dintre calculul descendent şi cel diferenţial.
Să facem acum o aplicaţie a acestei formule de coborâre a şirului compus. Să presupunem dat şirul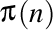 
al numerelor prime şi să calculăm coborâtul şirului compus 
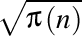, aplicând formula de coborâre a şirului compus determinată anterior. Aici avem că 
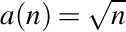şi, respectiv, 
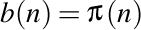. Atunci, 
.
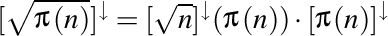Cum
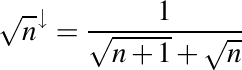
şi cum simbolic trebuie să înlocuim în această expresie pe 
cu 
şi pe 
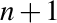cu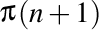 
, rezultă că
.
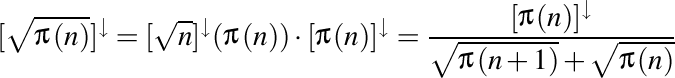În treacăt spus, conjectura lui Andrica afirmă că această expresie este mai mică decât unitatea. Observăm astfel că dacă am cunoaşte coborâtul şirului de numere prime, atunci am avea o posibilitate în plus de a verifica şi conjectura lui Andrica.
Niciun comentariu:
Trimiteți un comentariu
Comentariile vor fi moderate în măsura timpului meu disponibil, după care vor apărea pe blog. Voi încerca să public doar comentariile consistente sau interesante sau adevărate sau corecte sau la obiect. Voi căuta să le elimin pe cele din care nu avem nimic de învățat sau pe cele care afectează negativ mintea cititorului sau reclamele fără legătură cu blogul. De asemenea, voi face tot posibilul să răspund la comentariile care cer un răspuns. Vă mulţumesc pentru efortul vostru de a scrie în lumina acestor consideraţii!